関数データ解析（Machine Learning Advent Calendar 12/23）

前置き

この記事はMachine Learning Advent Calendarの12/23分の記事です。
大変申し訳ありません。時間切れでまとまっていないため、随時アップデートしていく予定です。

関数データ解析

福水先生の本をたまたま読んでいた際に出てきた「関数データ解析」という分野に少し興味を持ったので紹介させて頂きたいと思います…が、時間の都合上、詳細および「普通のデータ解析と比べてどう嬉しいのか」という話はまた次の機会とさせて頂ければ…と思います。
というかそもそも機械学習ではないのでは？という気もしますが、そこはご容赦ください。

関数データ

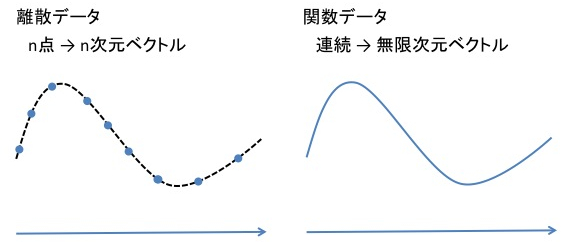
これは読んで字のごとく、関数そのものとして与えられたデータのことです。通常のデータ解析では各データはベクトル $\bf{x}$ として与えられ、データ集合 $\{\bf{x}_i\}$ に対して様々な分析を行いますが、関数データ解析では、各データは(ある区間で定義された)関数 $f_i$ として与えられ、データ集合 $\{f_i\}$ について通常のものと同じ解析を行うことを目的とします。

「関数データ」というのは、直感的には「(連続)無限次元のデータ」と思うことができます。もちろん関数が $\mathcal{R}$ 以外の値域を持つ場合などはイメージが難しくなりますが、そういう場合でも、関数たちの属する空間に一定の構造が定義されていれば分析ができる、というのが関数データ解析のいいところであり、抽象化を行う意義と言えます。

なぜ関数データか？

人間が具体的に扱える対象は高々可算個のデータであるため、関数データと言っても実際には離散的な点の集まりとしてしかデータを得ることができません。従って、関数データ解析を行うためには

離散点 $f_i^k, k=1,\cdots,K$ からなるデータの集合 $\{f_i = \{f_i^k\}\}$ を手に入れる
関数データを表現するための基底 $\{\phi_j\}$ を選ぶ
各離散データ $f_i^k, k=1,\cdots,K$ を関数データ $f(x) = \sum_j \alpha_j \phi_j(x)$ へ変換する

というような手続きが必要になり、「じゃあ結局データ点を普通にベクトルに並べてやればいいんじゃないの？」となってしまいます。それでもあえて「関数データ」として考えるのは、「モデリングが考えやすいから」というのが大きな理由ではないかと思います（論文を量産したいから、とかもあるかもしれませんが）。
例えば時系列のような、本来連続であって一連の「時間の関数」であるようなデータは、離散的な点の集まりとみなしてマルコフ的な逐次モデルでモデリングするだけでなく、時間区間全体にわたった関数であると考えてモデリングすることで、また違った解釈が可能になるかもしれないということではないかと思います。

分析を行うための「構造」

データを分析するためには、(データの属する空間に入れられた)いくつかの「構造」が必要になります。例えば、データ同士の距離とかデータベクトル同士の内積とかそういったものです。関数データ解析では、データの属する空間が関数空間(L2空間とか)なので、数ベクトルのときほど自明な構造は思いつきづらくなります。
具体的には、和と差、および内積とそれによって定まる距離が定義できれば色々な分析が可能になります（たぶん）。このような関数空間はヒルベルト空間と呼ばれるもので、関数データ解析は通常の実数空間ではなく、ヒルベルト空間の上で分析を行うものと言えます。
詳細は例によって後日とさせてください。

Functional PCA(fPCA)

関数データ解析の例として、関数データに対する主成分分析であるfPCAという方法を紹介したいと思います。
通常のPCAでは標本相関行列
$\rho_{ij} = \frac{1}{N}\sum_k (x_k^i - \bar{x}^i) (x_k^j - \bar{x}^j)$
( $x^i$ は $x$ の $i$ 成分を表す)の対角化を行い、固有値・固有ベクトルを求めます。同じ考え方を関数データに適用すると、相関行列は相関関数となり
$\rho(s,t) = \frac{1}{N}\sum_k (f_k(s) - \bar{f}(s)) (f_s(t) - \bar{f}(t))$
となります。これは[-1,1]の値をとるs,tの関数となり、これを対角化する関数 $\phi$
$\int dt \rho(s,t) \phi(s) = \lambda \phi(t)$
を求めることでfPCAの固有関数を求めることができます。
ただし、多くの場合は関数データを表現する際に使った（有限個の）基底を用いて固有関数自体も展開してやることで、通常のPCAのように行列演算で解くこともできます（参考文献3-1）。